SMote methodology for producing artificial knowledge

The artificial strategy of extra minorities (SMote) was created to handle the issues of classroom imbalance in equipment studying algorithms. The thought is to not collapse from uncommon occasions earlier than executing a equipment classification algorithm. Nonetheless, in her coronary heart, the Smote algorithm (Chawla et al., 2002) is actually a method to simulate new artificial knowledge from actual knowledge.

This text views SMote algorithm specializing in artificial knowledge simulation geometry. As a result of I’m thinking about simulation (not classification), after I say, “knowledge”, I all the time imply the information we’re simulating. Historically, that is the category of minorities (uncommon occasions).

A later article will show how one can apply a easy sparked algorithm to SAS.

Fundamental algorithm of Smote

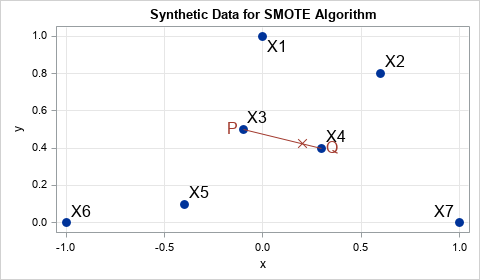
There have been many letters that describe modifications to the SMote algorithm, however the fundamental concept is to make use of linear interference between knowledge factors. In case you are given two true observations, P and Q, you’ll be able to generate a brand new artificial commentary by putting a random level within the line phase connecting P and Q. Within the type of the equation, the brand new artificial commentary is z = p + u*(QP), the place u ~ u (0.1) is a random uniform variet.

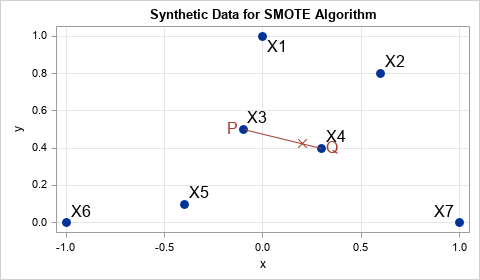
An instance is proven within the graph to the best. Factors X1, X2, …, X7 are knowledge factors. Level X3 is randomly chosen to be P. From the information factors close to P, level X4 is randomly chosen to be Q. then an artificial level (marked with an X) is chosen randomly alongside the road phase from P to Q.

There are alternative ways to pick P and Q. On this article, P will likely be chosen by acquiring random samples (with substitute) from the unique set of observations. After choosing P, you take a look at the farther neighbors of P, the place Ok is a parameter within the Smote algorithm. (The unique newspaper makes use of ok = 5.) ​​Level Q is chosen by these closest neighbors. On this article, q will likely be uniformly chosen by likelihood from the closest neighbors.

A smoked algorithm

As described above, the Smote algorithm makes use of linear interpolation among the many nearest neighbors to simulate artificial knowledge. For simplicity, I assume that each one variables are steady.

1. Enter an information matrix N x D, X. The traces of x are the d-dimensional factors used to generate artificial knowledge. We’ll point out the factors in accordance with their row quantity: x1, x2, …, xn.
2. Specify Ok, variety of nearest neighbors, the place 1 ≤ ok ≤ N. For every x_ICalculate factors Ok which can be closest to x_I on the Euclidean distance. For effectivity, you’ll be able to calculate the closest neighbors as soon as and keep in mind that info.
3. Specify T, the variety of new artificial knowledge factors you need to generate.
4. Select r rows uniformly at random (substitute) from group 1: n. These characterize factors “P”, which decide one finish of a line phase.
5. For every level, P, choose a degree uniformly randomly from the Ok neighbors closest to the P. these characterize the “Q” factors, which decide the opposite finish of a line phase.
6. For every get together, P and Q, generate a random uniform variants at interval (0.1). The brand new level of artificial knowledge is z = p + u*(QP).

The geometry of smote

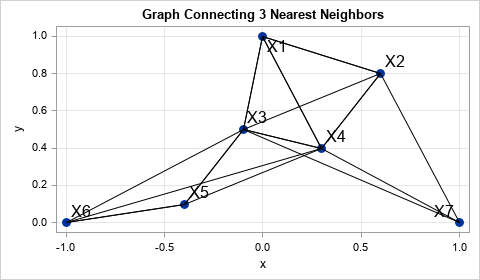
A serious geometric reality is that Smote generates artificial knowledge solely in line segments that join the unique knowledge. Artificial knowledge appear to be “spokesmen” emanating from a middle. In different phrases, the likelihood density for artificial knowledge depends solely on one-dimensional line segments. That is totally different from different strategies for producing multivarian knowledge. For instance, regular multivarian distribution has a density perform whose help is D-dimensional. Rasual variations can seem anyplace in a D-dimensional area.

The road segments within the graph beneath are the doable locations of SMote artificial knowledge generated from seven factors to 2-D. For this instance, Ok = 3. Artificial knowledge should be displayed in line segments connecting observations with their nearest neighbors.

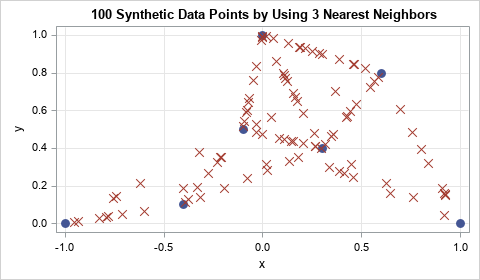
Artificial knowledge 2-D by smote

The graph beneath exhibits 100 factors of artificial knowledge generated by the seven unique knowledge factors when Ok = 3. The unique knowledge is represented by seven round markers. Indicators ‘x’ characterize artificial knowledge. I’ve eliminated line segments, however you’ll be able to clearly see that artificial knowledge seem alongside the road segments.

Artificial knowledge for Iris 4-D knowledge

To date, the examples have been two-dimensional, however the SMote simulation methodology works for greater dimensions knowledge. Well-known Iris Fisher (Saselp.iris in SAS) knowledge group has 50 observations belonging to class species = “versicolor”. Each commentary information the size and top of the petals and sepals of a flower. I run the smote algorithm with ok = 5 neighbors closest to generate 100 artificial knowledge values ​​from Iris versicolor knowledge measurements. The next manufacturing (from Proc Corr) exhibits easy descriptive statistics and hyperlinks between variables within the unique knowledge and within the artificial pattern:

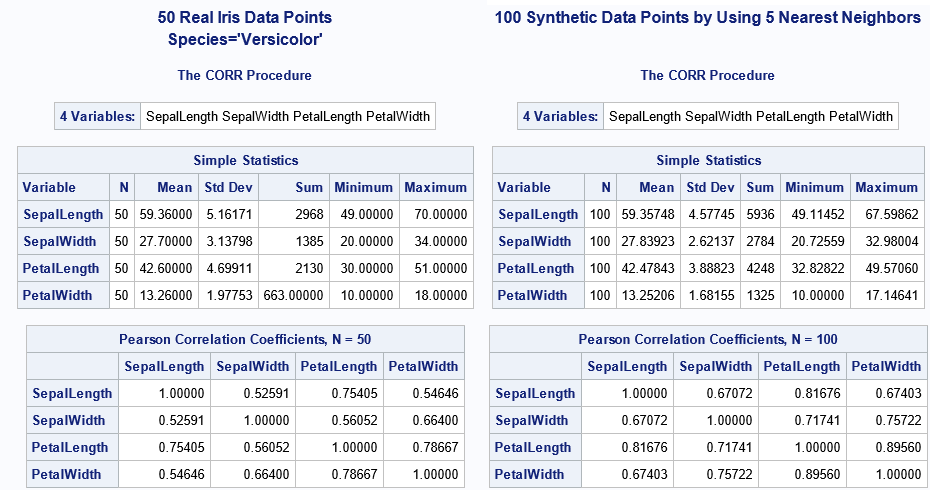
Actual knowledge statistics are proven on the left; Statistics for artificial knowledge are on the best. Though statistics are typically shut, there are some vital modifications in statistics, which I’ll focus on in a subsequent article.

Briefing

Smote was created to handle classroom imbalance issues in equipment studying algorithms. However some folks use Smote algorithm to simulate new artificial knowledge. This text gives a Simulation Abstract utilizing the SMote algorithm. I’ve not carried out a critical research that compares the statistical properties of actual and artificial properties, however algorithm geometry means that artificial knowledge will are inclined to have smaller variants and bigger correlations.

Appendix: Extra feedback about the usage of SMote algorithm for knowledge simulation

To stop the article from being too lengthy, I moved two subjects of dialogue on this appendix: How the scaling of variables impacts the smote algorithm and the way to decide on Ok, the variety of the closest neighbors.

Scaling and Standardization:Euclidean distance is used to calculate the closest neighbors. When all variables are steady, this has intuitive that means. If some variables are usually not measured in the identical unit, it’s best to standardize the variables. The examples on this article require no standardization methodology, however in apply the levels of variables are vital as a result of they decide which observations are shut to one another. In case you measure an inch size, the euclidian distances between the measurements are smaller than if you happen to measure the size in centimeters. Thus, the smoked algorithm depends upon the scaling of the information. In case you are utilizing the SMote algorithm, I encourage you to standardize steady variables utilizing a robust diploma of scale.

Selecting the variety of nearest neighbors:For a lot of knowledge teams, it’s not clear how to decide on the variety of the closest neighbors utilized in Smote. Chawla et al. (2002) used ok = 5, however the selection depends upon the dimensions and distribution of the information. Sometimes, Ok is small in comparison with the dimensions of the information, N. (equally, the Ok/N ratio is small in comparison with 1.) That is because of the first legislation of Tobler’s geography, which says “the whole lot has to do with the whole lot else however near issues than distant issues”. Related issues are current within the Ok-means grouping and within the Loess fashions, to say solely two examples. In these and different functions, it might be value contemplating Ok as a hyperparameter that may be allotted by choosing totally different values ​​of ok and see if the statistical properties of artificial knowledge are just like the related properties in unique observations.