How to add a curve to a diagram of the moment report

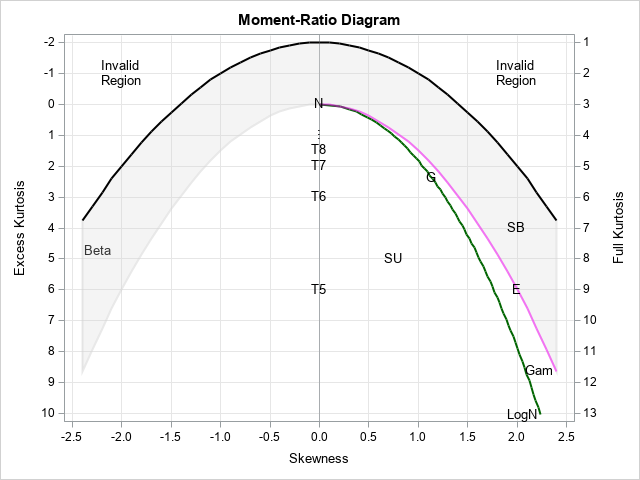
I have previously written about the moment’s report diagram as a graphic tool for modeling univarian distributions and also as a tool to examine the distribution of sketchs and curtosis statistics for distributions. Simple Diagram of the Moment Report (MR) from my book (Wicklin, 2013, Simulation of data with SASChapter 16) is shown to the right. The SAS Diagram Creating Program is described in Appendix E, which is available for free online. The simple MR diagram shows the possible values ​​of sketch and curtosis for some distribution, including normal (N), T (T5, T6, T7, …), Gumbel (G), Exponential (E), Gamma (GAM), Lognormal (Logn), Beta, and Flexible Johnson system (SU)

A SAS programmer arrived because he wanted to model univarian data using a probability distribution not shown in the diagram. He wondered if it is possible to add additional turns to the moment’s report diagram? The answer is yes! This article shows how to add a sketchy -kkurosis curve for distributing weibull in an MR diagram. Curves for other distribution can be created similarly.

Get the SAS program to create a report of the moment report

You can download the SAS code to create a report of the moment report from GitHub. If you want to follow together, download that file and execute it. For example, if you download it to the Define_Moment_ratio.sas file, you can execute the program using the statement included %, as follows:

%include "define_moment_ratio.sas";   /* specify a full path, such as "C://define_moment_ratio.sas" */

When executing the program, it creates a set of data and a macro:

• Creates a set of SG record data called “Anno”, which contains curves, points, regions and labels for the moment report diagram.
• Defines a macro called %plotmrdiagram. You can call the macro as
  
  %Fullmdiagram (DS, Anno, Transparency = 0)
  
  To overlap the points on the skewheness-Kurtosis plane in a diagram of the moment report. In the macro call, the input group (DS) must contain a variable called SKEW and a variable called Kurt. Anno argument is the SG record data set that is created by executing the program.

In this article, you will learn how to modify the record data set for the MR diagram. Specifically, I will show how to add a webull distribution curve.

Why use the moment’s report diagram?

There are some applications of the moment’s report diagram, but a popular is to help you select a distribution to model your data. To do this, you plan sketch and the data sample in the diagram. For example, assume that you have some data for which sample calculation and (excess) Kurtosis is calculated as sketch = 1.0704 and Kurtosis = 1,3983. The following step of the data creates a set of data with these sample moments, then overlaps the values ​​in an MR diagram:

/* Display a moment-ratio diagram */
data SK;
Skew = 1.0704; Kurt = 1.3983;
run;
 
title "Moment-Ratio Diagram for Sample";
%PlotMRDiagram(SK, Anno);

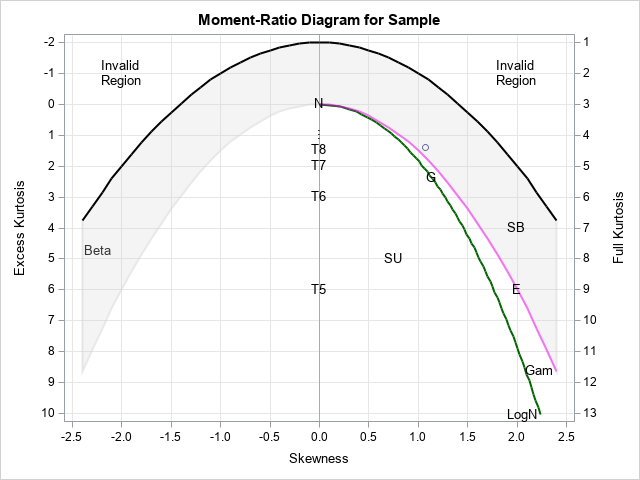
Moments of the sample are shown by a nearby marker (1.1, 1.4). (Note that the vertical axis, according to the convention, indicates down to an Mr. diagram) the location of the marker shows possible distributions that may be useful to model the data. In this case, the marker is close to the distribution of the gamma (the magenta line), the lognormal curve (the green line) and the Gumbel distribution (letter “G”).

However, the simple MR diagram does not contain any possible distribution. SAS programmer who wrote to me indicated that these data are often modeled using a weibull distribution, which is not shown in the MR diagram. The next sections show how to add a curve to the distribution of the Weibull to the MR diagram.

A look under the hood: How the MR diagram is built

Appendix of and Define_Moment_ratio.sas The file indicate how the MR diagram is built. If you look at Define_Moment_ratio.sas File, you will see that the MR diagram is drawn using a set of data data. Anno data group is the merging of some small data groups: one for the beta region, one for the lognormal curve, one for the gamma curve, etc. The code that builds the data group Anno looks like this:

data Anno;
  set Beta Boundary LogNormal GammaCurve MRPoints;
run;

Consequently, if we want to add more turns, we can imitate the existing code and add a new data set in the specified statement. The other section creates a note set of data called Weibulcurve containing the location of the moments for the distribution of the weibull.

Create a Weibull curve in the MR diagram

How do you add a webull curve to the MR diagram? I discuss how to do it in the Appendix of (Wicklin, 2013).

Eachdo curve is the image of a parametric function that designs a parameter value at a point in the sketch-cuktosis plane. There is no single symbol for the form parameter for the distribution of the weibull. Wikipedia article calls it deckAs Proc Univariate calls it Roof and documentation for the PDF function in Sas calls it A. I will use the Wikipedia note because the Wikipedia article includes formulas for sketchs and Kurtosis as a form of form parameter. Note: Wikipedia article also includes a degree parameter, λ, but sketch and curtosis are unchanged for scaling. Therefore, you can put λ = 1 in the Wikipedia formulas.

The following macro copies Wikipedia formulas to SAS. You can use macro in a data step that step through the values ​​of deck parameter in the range (0.9, 10). Technically, you must design the entire intervaldeck | deck ∈ (0, ∞)} in the sketch-curated plane, but experimentation indicates that deck <0.9 leads to extreme values. Moreover, as deck approaches infinity, the curve of sketch-Kurba approaches a border crossing point.

/* Formulas for skewness and kurtosis of Weibull distribution from Wikipedia:
   https://en.wikipedia.org/wiki/Weibull_distribution
*/
%macro SkewExKurt(k);
   mu = Gamma(1 + 1/k);                         /* mean (lambda=1) */
   var = (Gamma(1 + 2/k) - Gamma(1 + 1/k)**2);  /* variance */
   sigma = sqrt(var);                           /* std dev */
   skew = ( Gamma(1 + 3/k) - 3*mu*var - mu**3 ) / sigma**3;
   y1 = ( Gamma(1 + 4/k) - 4*mu*sigma**3*skew - 6*mu**2*var - mu**4 ) / var**2;
   x1 = skew;
   y1 = y1 - 3;                                 /* excess kurtosis */
%mend;
 
/* Compute the skewness-kurtosis curve for the Weibull distribution for various values of k.
   Experiments show that k < 0.9 results in the (skew,kurt) curve being too extreme.
   The image of the function for k in (0.9, 1000) traces nearly the full curve.
*/
data WeibullCurve1;
keep k x1 y1;
label x1="Skewness" y1="Excess Kurtosis";
k0 = 0.9;
k_infin = 1000;
do k = k0 to 10 by 0.2, 50, 100, k_infin; 
   %SkewExKurt(k);
   output;
end;
run;
 
title "Skewness and Excess Kurtosis Curve for Weibull Distribution";
title2 "k in (0.9, 1000)";
proc sgplot data=WeibullCurve1;
scatter x=x1 y=y1 / datalabel=k;
   xaxis grid;
   yaxis grid reverse;
run;

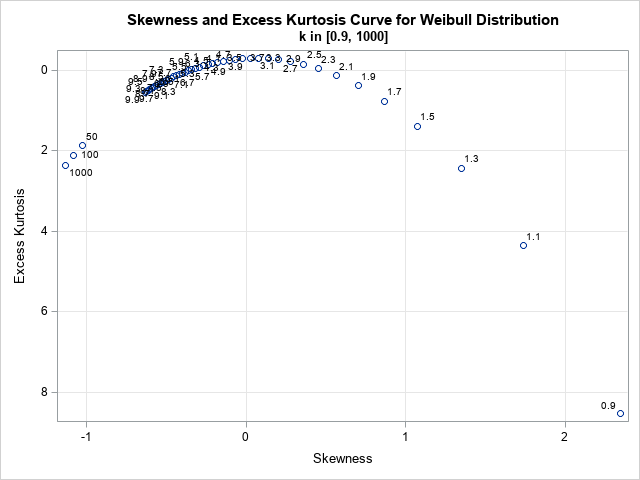
Instead of connecting the points, I have plotted them separately so that you can see that some points are widely separated while others are close together. I have labeled each point using the parameter value, deck. For simplicity, first generated points using a regular network at interval deck ∈ (0.9, 10). However, in the next program I use a good network of points for small values ​​of deck and a larger size Step to the greatest values ​​of deck.

Now that we know how to draw the curve of sketch values-Kurtosis for the distribution of weibull, let’s modify the previous MR diagram to include the new curve. To do this, use the polyline and polycont statements to draw the curve. The following program is a modification of examples in
Define_Moment_ratio.sas. By studying existing examples, you can understand how to draw the Weibull curve even if you are not familiar with the SG note object. Here is an implementation:

/* create an annotation data set */
data WeibullCurve;
length function $12 Label $24 Curve $12 LineColor $20 ;
retain DrawSpace "DataValue"
       LineColor "Brown"
       Curve     "Weibull";
drop k0 k_infin k mu var sigma skew;
k0 = 0.9; 
k_infin = 1000;
k = k0;
%SkewExKurt(k);
function = "POLYLINE"; Anchor="     ";
output;
function = "POLYCONT";
do k = 1 to 1.9 by 0.1,   /* use different step sizes for different intervals */
       2 to 5 by 0.25, 
       6 to 12,
       15, 20, 25, 50, 100, k_infin;
   %SkewExKurt(k);
   output;
end;
label = "Weibull"; function = "TEXT"; Anchor="Left ";
output;
run;

With this set of data data set, you can create the re-creation of the record data set that includes all the elements of the MR diagram as follows:

/* Add the new WeibullCurve data to the existing set of curves and regions: */
data Anno;     
  set Beta Boundary LogNormal GammaCurve WeibullCurve MRPoints;
run;
 
/* Draw the new moment-ratio diagram with the Weibull curve */
title "Moment-Ratio Diagram with Weibull Curve";
%PlotMRDiagram(SK, Anno);

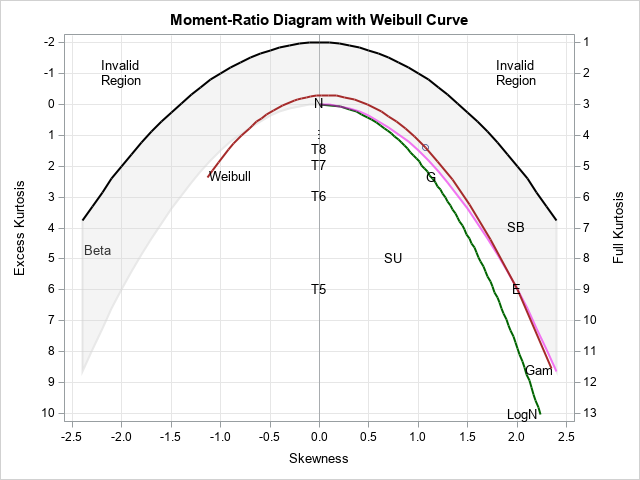
Brown curve is the set of sketch-tracked values ​​corresponding to the distribution of weibull with different parameter values, deck. The marker for the sample moments decreases exactly on the weibull curve, which indicates that weibull distribution is a suitable choice for a model.

Does the sample moment always come down to a curve?

I have to confess, when I specified the moments for the “sample”, I used the correct moments for a weibull distribution that has K = 1.5. Thus, the sample moment is in the weibull curve.

Usually, sample statistics are not exactly in the curve for the distribution of parents. In fact, an application of the MR diagram is to visualize the distribution of common samples of sketch and curtosis statistics. The following step of data simulates 100 samples of size n = 200 from the weibull distribution (K = 1.5). For each sample, you can calculate the sample moments and overlap them in the MR diagram:

/* simulate 100 samples of size N=250 from a Weibull(k=1.5) distribution (lambda=1) */
%let N = 200;
%let NumSamples = 100;
data Weibull(keep=x SampleID);
call streaminit(12345);
do SampleID = 1 to &NumSamples;
   do i = 1 to &N;
      x = rand("Weibull", 1.5, 1);
      output;
   end;
end;
run;
 
/* compute the skewness and kurtosis of each sample */
proc means data=Weibull noprint;
  by SampleID;
  var x;
  output out=MomentsWeibull skew=Skew kurt=Kurt;
run;
 
/* Display a moment-ratio diagram with a scatter plot in the background of 
   of the sample skewness and kurtosis for simulated samples. */
title "Moment-Ratio Diagram and Sample Moments for Weibull(k=1.5)";
%PlotMRDiagram(MomentsWeibull, Anno);

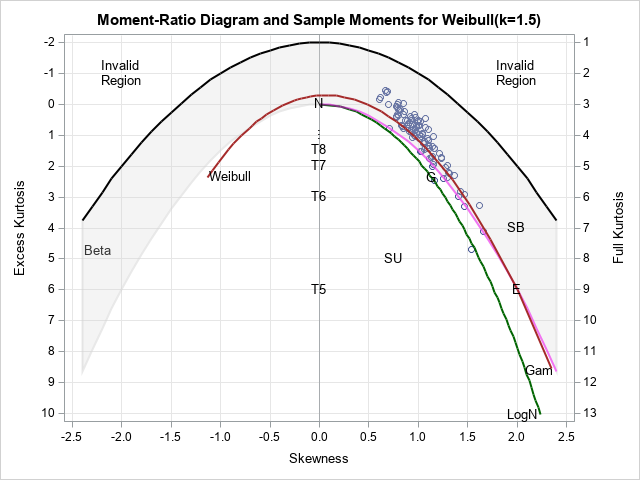
The MR diagram shows that the moments of the highest order sample are quite variable, even for moderately large samples with 200 observations. Yes, most of them are close to the Weibull Brown curve, but some are quite close to the gamma curve (Magenta) or the Log. This indicates that sample moments are often insufficient to set the best model. You need to add the MR diagram using specific knowledge of the domain, when existing, and other statistics such as maximum likelihood estimates.

Briefing

Appendix of e Simulation of data with SAS Shows how to build a simple diagram of the moment’s ratio. This article describes how to add a new curve to the MR diagram. This article adds the curve to the sketch curve-Kurtosis for the distribution of weibull, but the same ideas apply to other distributions, the shape of which depends on a parameter. You can download from the Github full SAS program that creates the graphs in this article.