Modulo operation for large integers in SAS

On social media, a SAS user reported that SAS could not calculate the module of an extremely large number. In SAS, the modulo operation is usually performed using the mod function, which calculates the remainder of the compartment of a integer, n, from a integer, d. (In symbols, the rest is r = mod (n, d).) When I asked for details, he directed me to a financial regulation showing how to implement an ISO algorithm to generate (and validate) a universal credit identifier (UL), which is a unique identifier used for financial transactions. One step of the algorithm requires finding the remains of a large number of 97.

After reading the regulation, it was clear why the SAS user had a problem, and it was also clear how to solve the problem. This article shows how to calculate the module operation in full arbitrarily large in SAS. In a subsequent article, I apply the full ISO algorithm to generate a control figure and certify a universal credit identifier (ul).

Problem with the mod of mod in full large numbers

Suppose you want to separate a integer (called dividend) from a positive integer d (called separator). Quotient Remener theorem (also called partition) states that there are unique positive number Q and r (quotes and rest) where r

In computer languages, we can use the floor function to calculate the quotes (floor (n/d)) and mod function to calculate the remainder (mod (n, d)). Documentation for the mod function in SAS states, “The calculation performed by the mod function is correct if both of the following conditions are true:

• Both arguments are full correct number.
• All integers that are less than each argument have accurate 8-Battal representations of the floating points. “

The last point of bullets states that n must be less than or equal to the constant ‘accuracy’, which for SAS is 900719254740992 ≈ 9.007e15. If we exceed that value, then the mod returns a lost value. The following data step shows the mod operation for a number less than, equal to and greater than the correct ‘constant’:

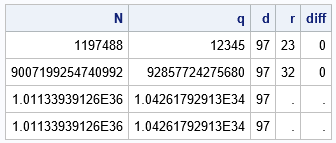
data Remainder_LargeInt;
format N q best16.;
input N;                 /* attempt to read dividend as integer */
d = 97;                  /* divisor */
q = floor(N/d);          /* integer part of quotient */
r = mod(N, d);           /* remainder */
diff = N - (d*q + r);    /* =0 for representable integers */
output;
datalines;
1197488
9007199254740992
1011339391255432926101144229991433300
1011339391255432926101144229991433338
;
 
proc print noobs; run;

For the first number, Quotient is 12345 and the rest is 23. For the second second number, which is the value of ‘accuracy’, the rest is 32. The mod function cannot calculate the remainder for two very long 37 digit numbers. Log Sas warns you there is a problem: Note: Invalid argument to operate mod (1,0113394e36.97).

The two full 37-digit numbers are examples from the ISO algorithm for generating a control figure and verifying a (and validant) generator of a universal credit identifier. The problem is that SAS converts these integers in pairs, and representation is incorrect due to the limits of the final 64-bit accuracy calculations, which holds 16 precise digits.

Interestingly, when you read the iso’s description, find out that these long integers are not stored as numbers. Rather, they are preserved as
character wirewhere each character is a figure 0-9. Verses are the unique identifier for a specific loan from a specific financial institution. Do you remember to press in the “Routing Bank” and “Account Numbers” when you transfer money to/from a bank account? Well, the full integers in this example are similar. They represent a union of an identifier for a financial institution and an account in that institution.

The algorithm in ISO regulation shows you how to generate these wires. But it also tells you that you have to calculate the value mod = (n, 97) where n is one of these long wires! Don’t you need to turn the string into a large number to calculate the remainder? No, you don’t!

Long Division Algorithm

In elementary school, students learn how to find quotes and the remainder by applying the long -dividing algorithm. The steps in that calculation dictate that you move from left to right along the dividend figures. You should never see the whole dividend! On the contrary, for each figure, you gradually build the quod by seeing a remainder from the previous step. Stepdo step requires only a small number, which is always less than 10*d. An example is shown to the right for the seven -digit dividend 1197488. The long division algorithm produced the remainder (and quit, if desired) in the most seven steps.

My pointing is this: you can perform the long division into a range of numbers without ever having to maintain the full dividend. You can perform the long -dividing algorithm by crossing the integers in the range from left to right. At each step, you keep track of the remainder, which is the number you “crash” when making long breaks on paper. In the next step, you multiply the remainder with the previous part with 10 (move the remaining left) and drop the next number from the dividend. You then understand the partial quod (which we do not need here) and the remainder.

Although the elementary school algorithm requires multiplication and discount, in a computer program you can replace them two steps with a single call to the mod function which gives the remainder at each step of the algorithm. This is illustrated to the right. You can safely use the mod operation in this algorithm because temporary dividends are never more than 10*97.

The following step of Procmp FCMP defines a function called mod_from_string. The function receives two arguments. The first parameter is a string (s) that contains only characters for digits 0-9. The second parameter is a complete separator (D), such as D = 97. The function applies the long -dividing algorithm to find the remaining mod (n, d). The only complex part is that you need to use the input function to return the digits into the dividend range.

proc fcmp outlib=work.banking.ULI;
   /* Compute the remainder of a large integer (represented as a string)
      when divided by d.
      This implements the standard long-division algorithm,
      but at the i_th step the i_th character is converted to an integer.
   */
   function mod_from_string(s $, d);
      r = 0;                       /* initialize remainder */
      do i = 1 to length(s);
         c = substr(s, i, 1);      /* i_th digit as character */
         digit = input(c, 1.);     /* i_th digit as integer */
         r = mod(10*r + digit, d); /* running remainder */
      end;
      return( r );                 /* return remainder as an integer */
   endsub;
quit;

With this new defined function, you can represent large integers as wire, which ensures that the module operation will be accurate for large numbers arbitrarily. The following example reads the same four integers as before, but this time it preserves numbers as verses. Call for mod_from_string calculates the remaining mode (n, 97).

option cmplib=work.banking;  /* set search path for the FCMP function(s) */
 
/* test the mod_from_string function by using the examples in 
   https://www.consumerfinance.gov/rules-policy/regulations/1003/c/
*/
data Remainder_LargeStr;
length ULI $200;    /* "N": represent the integers as a string of character digits */
input ULI;
r = mod_from_string(ULI, 97);   /* remainder mod 97 */
datalines;
1197488
9007199254740992
1011339391255432926101144229991433300
1011339391255432926101144229991433338
;
 
proc print noobs; run;

Success! Production indicates that the program can perform the module operation on these wires. The residues for the first two numbers (23 and 32) are the same as calculated by the mod function. The large verses of the integers are taken from an example in the ISO regulation, so I know that the remains of 60 and 1 are correct.

Briefing

A SAS user noted that he had problems to calculate the module operation in extremely large numbers. The specific application was the remained 97 calculation of a large large number to use as a check. SAS documentation says the mod function works in a integer numerical number. Interest should be less than ‘accuracy’, which is the value of the largest integer that is exactly representative at a double precision vessel value. However, instead of maintaining the full full number as a value of double precision (and therefore loss of accuracy), you can write a short function that performs the algorithm with the long -range algorithm in the range. That way, you never need to deal with a large number.

You can use SAS to implement the entire algorithm that generates a “control figure” and proves a ul. I don’t want this post to get too long, so I will apply the rest of the algorithm in a special blog post.