Layered bootstapping and when we use it

When using bootstrap method in statistics, it is called the most common method of reset the revival of the matter. For data that has observations, each bootstrap sample is created by replacing n (or “cases”) samples in data. However, if the data set includes categorical variables, it may be necessary to perform the layered resettlement In place, this article shows how to perform samples layered in SAS and discusses two situations in which laying samples is a better way to build bootstrap samples.

When is the sampling of layered samples appropriate?

As stated in the documentation for Surveyselect Proc in SAS, if the population is divided into non -supernatural subgroups (called layer), you can use layered samples to choose from each layer independently. In the context of the bootstrap, any bootstrap reset will contain subgroups of the same size as in the original data.

Researchers use layered samples to choose random population samples when they suspect that a variable of interest varies throughout the layers or when there are very small sub -industries that are important to be represented in data. For example, a researcher may suspect that a health result depends on the race. She knows that about 2.9% of the population is identified as local American. She is worried that if she recruits 200 cases at random, the sample may not have a proper number of local Americans in the study. By deliberately recruiting locals-Americans for the study, it can ensure that it has data on that sub-policy.

As a rule, if the data is collected using a layered sample, then you should use the layered sampling when you start the data. There are two reasons for this:

• “Small sub -policy problem” can affect statistical assessments in bootstrap samples. For example, if your data set contains 200 observations and only a few local Americans, the usual reset of the issue will result in some bootstrap samples that have native American zero in them.
• Bootstrap repair should follow the data generation process as close as possible. This applies to both layered models and nest patterns. For example, if original data student samples within classes within schools, bootstrap samples should be similarly built. The use of layered samples is sometimes called a “design -based sampling” method because each bootstrap sample reflects the design of the study.

A GLM analysis of a small data located in SAS

If you are not familiar with the bootstrap way in SAS, read “The essential guide for bootstrapping”. For this article, let bootstrap a 90% confidence interval for regression coefficients in a simple linear group Anova model y ~. First we will perform a conventional bootstrap analysis, which uses sampling with replacement, then compare that analysis with the results of a layered bootstrap sampling method.

Example data are small (n = 20) and have a response variable (Y) and a category variable (group). The group variable has three levels: group = ‘a’ (n1 = 8), group = ‘b’ (n2 = 4), and group = ‘c’ (n3 = 8). The following SAS statements create data and graph the Y variable against group levels. (Variable X is not used in this article.)

data Sample;
input Group $ x y @@;
datalines;
A 6.2 120.0 A 4.6 108.7 A 3.2 101.4 A 5.0 110.7 
A 6.0 125.3 A 6.9 123.8 A 4.9 126.2 A 5.3 114.7 
B 7.8 149.3 B 6.4 119.5 B 6.1 111.5 B 5.8 111.0 
C 5.9 106.4 C 7.8 96.1  C 6.3 111.1 C 7.4 109.5 
C 6.1 109.5 C 9.2 111.7 C 7.4 114.7 C 6.8 105.5 
;
 
title "Distribution by Group";
proc sgplot data=sample noautolegend;
   vbox y / category=Group nofill;
   scatter x=Group y=y / markerattrs=(symbol=CircleFilled);
run;

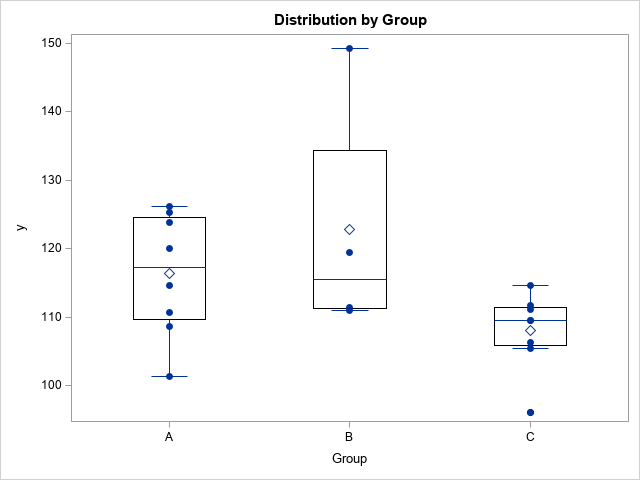
The graph indicates that the average group changes. The following call to PRO GLM adapt to the coefficients for a simple ANOVA model and uses asymptototic assumptions to evaluate a 90% confidence interval for each parameter:

title "ANOVA: Parameter Estimates and CIs";
proc glm data=Sample plots=none alpha=0.1;
   class Group;
   model Y = Group / solution clparm;
quit;

In GLM analysis, the ‘C’ group is the reference group. 90% trust interval for group coefficient = ‘a’ contains 0, but simply barely. Due to the small size of the sample (especially in the ‘B’ group), you can decide that the intervals of asymptotic belief are not appropriate. One alternative is to use a bootstrap analysis to evaluate confidence intervals as the percentages of parameter estimates from a large number of ANOVA models directed at Bootstrap Resamples.

A summary of conventional bootstrap sampling in SAS

I have previously discussed how to perform by restoring issues to bootstrap a regression model in SAS. You can use the method Option = Urs in the Proc Surveyselect statement to generate 1000 bootstrap samples from the data:

%let NumSamples = 1000;       /* number of bootstrap resamples */
 
/* Conventional case resampling for generating bootstrap samples.
   If you do not use the STRATA statement, the number of observations
   for each level of the categorical variables will vary in the bootstrap samples */
proc surveyselect data=Sample NOPRINT seed=123
     method=urs              /* resample with replacement */
     samprate=1              /* each bootstrap sample has N observations */
     OUTHITS                 /* use OUTHITS option to suppress the frequency var */
     reps=&NumSamples        /* generate NumSamples bootstrap resamples */
     out=BootCases(rename=(Replicate=SampleID));
run;
 
/* perform the conventional bootstrap analysis where the num obs for each level varies */
title "Bootstrap Distribution of Regression Estimates: Case Resampling";
ods select none;
proc glm data=BootCases plots=none;
   by SampleID;
   class Group;
   model Y = Group / solution;
   ods output ParameterEstimates = PECases_long;
quit;
ods select all;
 
proc means data=PECases_long mean stddev P5 P95;
   class Parameter;
   var Estimate;
   ods output Summary=Case_summary;
run;

In CIS bootstrap estimates, CI for group coefficient = ‘A’ does not contain 0. In addition, the CI coefficient for the group = ‘b’ is significantly wider than the EC GLM interval rating.

Note that the result from the ProC means reports that group statistics = ‘b’ are calculated using 986 observations, not 1,000! This is because 14 samples do not contain any observation from the ‘B’ group. This is further explained in the rest.

Bootstrap ratings in small subgroups

Production from Proc means that 14 bootstrap samples contain no observation from the ‘B’ group. Let’s look closer to the size of the subgroup ‘B’ in the bootstrap samples.

Original data have four observations in subgroup ‘B’. In the bootcase data group, there are 1,000 samples of size 20. Among the bootstrap samples, the number of observations in subgroup ‘B’ will change. In some samples, the subgroup ‘B’ will contain 4 observations, while other samples may have subgroups of size 3 or 5. The following graph indicates the proportion of samples for which subgroup ‘B’ contains 0, 1, 2, 11 observations.

Some samples of bootstrap (14 out of 1,000, or 1.4%) contain no observation from the ‘B’ group. The appendix shows how to use primary probability theory to prove that, in general, you should expect about 1.15% of bootstrap samples to contain zero observations from the ‘B’ group. So this example is in agreement with the theory.

Layered bootstrap sampling in SAS

If you have used layered samples, each sample contains eight observations from the ‘A’ and ‘C’ groups and four observations from the ‘B’ group. Let’s see how to apply the sampling layered in SAS.

The first step is to order the original data according to the layer variables. The statement of the layers is like the statement with: it makes the survey procedure do the same (resurrection) for each level of the categorical variable you listed in the layer statement. Let us demonstrate this fact by generating 1000 bootstrap samples using RI -occasional production:

/* to use the STRATA statement in PROC SURVEYSELECT, sort the data by the categorical variables */
proc sort data=Sample;
   by Group;  /* put other categorical variables here, if necessary */
run;
 
/* If you want to preserve the number of obs in each level of one or more categorical
   variables, list the variables on the STRATA statement */
proc surveyselect data=Sample NOPRINT seed=123
     method=urs              /* resample with replacement */
     samprate=1              /* each bootstrap sample has N observations */
     OUTHITS                 /* use OUTHITS option to suppress the frequency var */
     reps=&NumSamples        /* generate NumSamples bootstrap resamples */
     out=BootDesign(rename=(Replicate=SampleID));
strata Group; /* put other categorical variables here, if necessary */
run;
 
/* to perform BY-group processing, sort the data by the SampleID variable */
proc sort data=BootDesign;
   by SampleID Group; /* put other categorical variables here, if necessary */
run;
 
/* perform the bootstrap analysis where the num obs for each level is always the same */
title "Bootstrap Distribution of Regression Estimates: Stratified Resampling";
ods select none;
proc glm data=BootDesign plots=none;
   by SampleID;
   class Group;
   model Y = Group / solution;
   ods output ParameterEstimates = PEDesign_long;
quit;
ods select all;
 
proc means data=PEDesign_long mean stddev P5 P95;
   class Parameter;
   var Estimate;
   ods output Summary=Design_summary;
run;

In this analysis, each bootstrap sample contains exactly four observations from the ‘B’ group. You can see that the 90% bootstrap rating is based on 1,000 samples, not 986 as in the previous analysis. Moreover, stratified estimates result in smaller ones because there are fewer changes in the size of under -branches.

Briefing

This article discusses bootstrap sampling when data contain categorical variables representing sub -policy. If you think that data characteristics vary in the sub -policy, you may want to use sampling layered within the subgroups instead of a sampling method that allows the size of the subgroups to vary between bootstrap samples. If the data has one or more small subgroups, the laying samples eliminates the situation when some bootstrap samples contain zero observations from the small subgroup.

Appendix: Percentage of bootstrap samples that will not contain any observation for a subset

Remember that the group = ‘b’ has four observations and all the data is the size n = 20. Thus, the group ‘b’ consists of 4/20 = 1/5 of the observations. Q: If you select 20 observations from the data randomly with the replacement, what is the probability that the data does not contain any of the observations from the group = ‘b’?

Let’s calculate the answer. The probability is 1/5 that the first observation is chosen by the group = ‘b’, so the probability is 4/5 that the first observation is not from ‘b’. Because we examine it with replacement, the probability is the same for any other observation you choose. From the independence of the process, the probability is (4/5)²⁰ 0.0115 ≈ that the sample does not contain an observation from the ‘B’ group.

This is a little probability. However, in a bootstrap analysis, we do not only generate a bootstrap sample, we generate a large number such as 1,000 or even 10,000. If you generate a large number of bootstrap samples using replacement sampling, you should expect 1.15% of them not to contain any observation from the ‘B’ group.